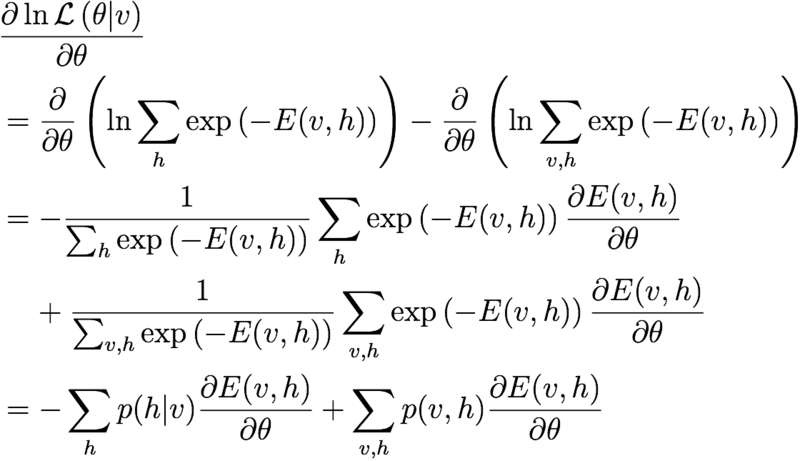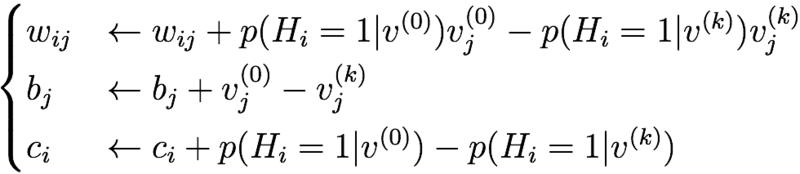ICML2013:疎行列の固有ベクトル計算(sPCA)読んで実装した
大昔に書いた下書きを発見したので公開
論文
Fast algorithms for sparse principal component analysis based on Rayleigh quotient iterationVolodymyr Kuleshov著
概要
疎行列の固有ベクトルを、レイリー商を使う事により高速に解く。著者によると、既存のSparse Principal Component Analysis(sPCA)と比較しても、勝るとも劣らない精度で、1桁か2桁くらい計算量が少ないそうだ。
理屈上は、行列の行数(=列数)をn、非ゼロ要素の数をkとして、イテレーション毎に
ちなみに既存手法には、べき乗法(PM)とか、半正定値計画問題(SDP)とか、Greedyな探索によるものとか、色々あるらしい。
10000×10000の疎行列(半正定値対象。ランクは3。密度は3*100*100/10000*10000=0.03%)を対象として実験してみた。
結果としてRのeigen関数と、この論文の手法で固有値分解した場合の速度を比較すると、200倍ほど速い。(10秒:1800秒)
自分で書いたゴミコードなので、もっと頑張れると思う。
レイリー商(Rayleigh’s quotient)とは
これを読むとよく分かる。
もうちょっと詳しく知りたい人、例題とか欲しい人はこっち。
要するに、二次形式の問題から発生した、行列の固有値に関する評価指標の一つで、微分すると一般化固有値問題が出てくるものである。
本論文では、行列がスパースなため、こいつを利用し、固有ベクトルに関してL2とL0ノルムで制約しつつ求める。
特徴(飛ばして良いところ)
sPCAにおいて、最も一般的なのは、2010年に出たGPM(Generalized Power Method)と呼ばれるものである。
これは他の既存手法と比較して、同等以上の性能を誇る。
GPMは二次形式の問題を勾配法で解いている。
(さらに疎な行列の特性と、べき乗法を使って加速しているっぽい)
したがって原理としてとても簡単で直感的なものとなっているものの、対象となる行列が大きいと収束が遅い。
対して本論文の手法GRQI(Generalized Rayleigh Quotient Iteration)は、QR分解にも使われるレイリー商を、ニュートン法みたいな二次収束する最適化によって解く。
したがって早くて当然という論法。
具体的な理屈

これを上から順に解説していく。
Algorithm1 GRQIでは、イテレーション(反復)毎にレイリー商とべき乗法による更新する。
そして結果得られる固有ベクトルを、Euclidean Projectionする。
EPの日訳がよく分からないが、要するにL0とL2の正則化が作る超平面(というか球)に対して、射影する。
詳しい理屈はこちら
- レイリー商の計算
レイリー商は、定義より以下のように求められる。
余計な計算をしたくないので、固有ベクトルxの非ゼロ要素のみを抜き出す。
ゼロの要素は、積をとってもゼロのままなので無意味。 - レイリー商の更新
どういうことかと言うと固有ベクトルを利用して、行列は対角化できる。
この原理を利用する。
- べき乗法の計算
べき乗法とはこういうもので、
要するに、行列を何回もかけて、高速に最大固有値と固有ベクトルを求める方法である。 - Euclidean Projection
要するに、制約条件を満たす範囲への射影である。
今回の場合、固有ベクトルの要素の内、絶対値が大きいものからk個のみを採用して、残りをゼロにすれば良い。
以上の原理により、非ゼロ要素のみに注目して、固有ベクトルを高速に求めるのが、本手法である。
ソースコード
#generalized Rayleigh quotient iteration #固有ベクトルを求める際にレイリー商を使う方法の一般化 #固有ベクトルの導出 grqi <- function(Sig,x.new=NULL,k=3,J=2,e=0.01,END=100){ if(is.null(x.new)){ x.new <- matrix(1,nrow=dim(Sig)[1],ncol=1) } for(i in 1:END){ #keep old vec x.old <- x.new #compute rayleigh quotient and working set mu <- c( (t(x.new) %*% Sig %*% x.new) / (t(x.new) %*% x.new)) w <- which(x.new != 0) if(length(w) == 0){ break } #rayleigh quotient iteration updata sol.mat <- svd(Sig[w,w] - mu * diag(1,nrow=length(w), ncol=length(w))) sol.diag <- 1/sqrt(sol.mat$d) sol.diag[sol.diag > 10^10] <- 10^10 ##これを作らないと1*1行列でバグる tmp.diag <- matrix(0,nrow=length(w),ncol=length(w)) diag(tmp.diag) <- sol.diag sol.mat <- sol.mat$u %*% tmp.diag %*% t(sol.mat$v) x.new[w,1] <- matrix( sol.mat %*% as.matrix(x.new[w,1]), nrow=length(w), ncol=1) x.new <- x.new / sqrt(sum(t(x.new) %*% x.new)) #power method update if(i < J){ vec <- matrix(Sig %*% x.new,nrow=dim(Sig)[1],ncol=1) x.new <- vec / c(t(vec) %*% vec) } #update v <- rep(0,dim(Sig)[1]) v[order(x.new,decreasing=TRUE)[1:k]] <- 1 x.new <- x.new * v x.new <- matrix(x.new / sqrt(sum(x.new * x.new)),nrow=dim(Sig)[1],ncol=1) if(sum(is.nan(x.new)) > 0){ break } if( sum((x.new - x.old)^2) < e){ break } } return(x.old) } #sparse principal component analysis(疎行列PCA) spca.grqi <- function(Sig,k=NULL,J=100,e=0.01,K=NULL,d=1,END=100,DIAG=FALSE){ #Sig:データの行列(半正定値対象) #k:一つの固有ベクトルに現われる非ゼロ要素数 #J:べき乗法の使用頻度(Jが大きいほど高速で雑) #e:許容誤差 #K:求める固有ベクトルの数 #d:固有ベクトルの重複を制御する(d=1で重複なし) #END:ひとつの固有ベクトルの最大更新回数 #DIAG:固有値計算(データを複製するのでメモリを消費する) if(is.null(K)){ K <- dim(Sig)[2] } if(is.null(k)){ k <- dim(Sig)[2] } if(DIAG == TRUE){ data <- Sig } egn <- matrix(0,nrow=dim(Sig)[1],ncol=K) for(j in 1:K){ i <- which.max(colSums(Sig)) x.0 <- matrix(Sig[,i],nrow=dim(Sig)[1],ncol=1) x.k <- grqi(Sig,x.0,k,J,e,END) egn[,j] <- x.k Sig <- Sig - d * c( t(x.k) %*% Sig %*% x.k) * (x.k %*% t(x.k)) } ans <- list(egn) names(ans) <- c('vectors') if(DIAG == TRUE){ values <- solve(egn) %*% data %*% solve(t(egn)) ans[[2]] <- values names(ans[[2]]) <- c('values') } return(ans) } #使い方 if(FALSE){ #普通の行列に対する精度の確認 ##データの生成 data <- matrix(1:25,nrow=5,ncol=5) data[lower.tri(data)] <- t(data)[lower.tri(data)] ##処理 ans.spca <- spca.grqi(data, k=dim(data)[2], J=100, e=0.00001, K=5, d=1, END=1000, DIAG=TRUE) ##精度確認 print(sum((ans.spca[[1]] %*% ans.spca[[2]] %*% t(ans.spca[[1]]) - data)^2)) #疎行列に対する速度の確認 ##データ生成 data <- matrix(0,10000,10000) data[1:100,1:100] <- 1 data[101:200,101:200] <- 10 data[201:300,201:300] <-5 ##処理 system.time(ans.spca <- spca.grqi(data, k=dim(data)[1], J=100, e=0.001, K=3, END=1000, DIAG=FALSE)) ##eigenとの比較:30分くらいかかるのでおすすめしません ##sysytem.time(ans.egn <- eigen(data)) ##固有ベクトルの確認 image(log(sqrt(ans.spca[[1]]))) }
ゼロから始めるDeepLearning_その4_Restrictedボルツマンマシンとは
はじめに
MNISTで全然うまく行かないことが発覚したので、最適化を調べ中きちんと動きました。
学部四年生向け。だった。
ニューラルネットワーク
→(AutoEncoder)
→(DenoisingAutoEncoder)
→ホップフィールドネットワーク
→ボルツマンマシン
→Restrictedボルツマンマシン(この記事)
→(Gaussian Binary - Restricted Boltzmann Machines)
→(DeepBeliefNetwork)
→(DeepNeuralNetworks)
→畳み込みニューラルネット(後日)
太線以外は読み飛ばしてOK
Restricted Boltzmann Machines(RBM)をとりあえず使ってみる
RBMには、ホップフィールドネットワークという前身がある。
できることは、それと同じである。
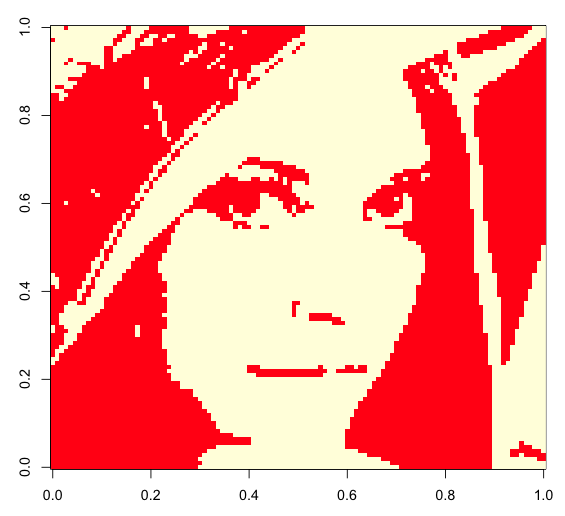
即ち、RBMとは、脳的なもの(マルコフ確率場)に、画像を複数覚えさせるものである。
1.画像を用意する(ノイズなしの元画像)
覚えさせる画像その2(CameraMan:111*111画素)

2.画像から結合係数wを学習する
焼きなまし法を用いて、上の2つの画像より、以下の結合係数wを学習する。
(ここでは4例を上げるが、実際には30*(111*111)の行列で、30例を上げることができる)
(結合係数wには、入力画像に近しいものがいくつもあるが、この理由は後述する。)
3.学習した結合係数wを用いて、ノイズ入り画像から元画像を復元する
ノイズ入り画像とは、以下の様なものである。
(ぱっと見、結合係数wと似てるけど別物。元画像+ノイズによって生成)
これをRBMの入力層→隠れ層→出力層(実際には入力層と同じ)と変換すると、ノイズなし画像が復元される。
実際に、結合係数wを用いると、ノイズ入りの画像から、以下の様な画像を復元することができる。
これらは、学習途中の結合係数wによるものである。
もっと学習回数を重ねた結合係数wを用いると、以下のような画像が復元される。
最終的には、鮮明な画像を復元可能な結合係数wが学習され、以下のように復元される。
概要・Restricted ボルツマンマシンってなに?
DeepLearning(DeepBeliefNetworks)で使われるのは、
Restricted Boltzmann machine(接続制限されたボルツマンマシン)と呼ばれ、
前章のホップフィールドネットワークの改良であるボルツマンマシンの特殊な事例と言える。
図的に書くと、以下の様なものである。
1.図中でvと書かれている可視素子(入出力を行う素子:visible unit)に、
{0,1}の2値で表現可能な入力画像を入れる。
2.可視素子vが結合係数wによって、隠れ素子h(hidden unit)に入力され、
その入力にしたがって生成される確率分布に従って、隠れ素子hが{0,1}の値を取る。
(σはシグモイド関数、cはバイアス)
3.今度は逆に、隠れ素子hが結合係数wによって、可視素子vに入力され、
その入力にしたがって生成される確率分布に従って、可視素子vが{0,1}の値を取る。
(この可視素子の出力が入力した元画像に一致することを期待している。)
(bはバイアス)
4.以上の工程から得られる確率が入力したvの分布に近づくように
パラメータを学習する。
(はパラメータw,b,cのこと)
5.学習し終わったRBMに元画像にノイズを加えた画像を入力すると、
ノイズがなくなった元画像が出力される。
あえてニューラルネット的に書くと、こんな感じになる。
この手法が作られたのは、以下の経緯による。
で表される入力画像は、
通り考えうる。
(入力は空間上のある分布から生成されている)
素子数をnとすると、ボルツマンマシンのパラメータの自由度はn(n+1)/2である。
(結合係数wijとしきい値θi)
ボルツマンマシンは空間中で、なおかつモデルの制約を満たす1つの分布を表現しているにすぎない。
(モデルが導入されているので、導入した構造によって自由度が下がっている)
この自由度の差を埋めるために、m個の隠れ素子という概念を導入する。
入出力用の素子はある意味、決まった値を取らなければならない。
隠れ素子にはそのような制約がなく、モデルを複雑化することができる。
隠れ素子の導入によってボルツマンマシンの自由度は(n + m)(n + m + 1)/2にまで増加する。
しかし、こういった素子を増やすと、過学習などが発生して大変なことになる。
ついでに学習コストも増大する。
しかたがないので、素子の接続をある程度制限することで、これらの問題を回避しようとした。
その結果生まれたのが、接続制限されたボルツマンマシン(RBM)である。
またこのRBMにおいて有名な最適化手法が、Hintonの作った
Contrastive divergence法というものであり、
これによって現実的なデータサイズに対する十分実用的な学習ができるようになった。
理論・Restricted ボルツマンマシン
以下、内容を説明するために色々な式が飛び交います。
実装だけできれば良い場合は、本ページ末尾にあるRのコードを写すか、
An Introduction to Restricted Boltzmann Machinesの28ページを読んで下さい。
ホップフィールドネットワークと同様に、エネルギー関数(評価関数)を定義する。
(隠れ素子がhとして分離されているだけで、同じ式)
このエネルギー関数は、可視素子
と隠れ素子
の積(相関)と、
結合係数が一致する時に、最も小さな値(最尤値)を取る。
(結合係数wには、入力画像に近しいものがいくつもあるのは、このエネルギー関数による)
またボルツマンマシンと同様に、素子の発火確率pの式を定義する。
具体的には、以下の様に、
したがって、各パラメータごとの勾配は以下のようになる。
よって、以下の更新を繰り返せば良い。
しかしここで問題となるのが、という項である。
とは、入力画像としてありうる{0,1}のパターン全体のことである。
つまり、指数オーダーで組み合わせ爆発を起こす確率分布を、
実際には存在しないデータも含めて計算しろと言われている。無理。
ここで普通は、十分長いギブスサンプリングを繰り返してを近似することを考える。
ただ、それには問題がある。
(以下Hinton, Geoffrey E.の翻訳)
ギブスサンプリングでは、確かに平衡分布を計算可能ではあるが、
そのサンプリングは、モデルが形成しうる分布の至るところから行われるため、一般に大きな分散を持つ。
この分散は、変な局地を作る。
また、このサンプリング結果は、モデルのパラメータにも依存する。
したがって、例えあるパラメータを取る時、勾配が0になるとしても、
サンプリングにおいて大きな分散を持つならば、そのパラメータは弾かれてしまう。
(所々が振動している平らな板に砂をばらまくと、振動していないところに砂が集まるイメージ。
今回問題となるのは、振動しているところが、実は時間平均を取ると、振動していない(勾配0)場合)
なので、Hintonは別のやり方を考えた。
Contrastive Divergence法である。
(Hinton, Geoffrey E. "Training products of experts by minimizing contrastive divergence." )
ある入力ベクトル(一枚の画像)をとする。
入力ベクトルを用いてk回後のサンプリングで得られたある1つの入力(出力)ベクトルをとする。
(このkは基本的に1で良い)
この2つを用いて、十分長いギブスサンプリングを繰り返した後のを近似すると、
対数尤度関数の微分は以下のようになる。
この手法は、平衡状態に至るまでギブスサンプリング(MCMC法)を用いて、
最初状態と最後の状態の導関数(微分)を比較するのではなく、
1ステップのマルコフ連鎖(サンプリング)によって、パラメータを更新する。
これによって、マルコフ連鎖にありがちな、最初の更新で初期分布から離れてさまよってしまう傾向を減らしている。
ざっくり言うと、この勾配が0になるのは、モデル(結合係数w)が完全な時のみなので、
この更新を繰り返して勾配がなくなったところを見れば十分という理屈。
したがって画像一枚ごとに、以下の更新を繰り返せば良い。
終了。
ちなみに、一番良くわからない隠れ層の素子数だが、
の空間における任意の分布は、
覚えさせる画像の数+1個の隠れ素子を用いることで近似できるらしい。
(Le Roux, Nicolas, and Yoshua Bengio.
"Representational power of restricted Boltzmann machines and deep belief networks." )
直感的には、結合係数wが(画像の種類×画像のピクセル数)の大きさを持っていれば、
結合係数w自体を画像そのものにすることで、すべての画像を記録できるためと思われる。
(冒頭の実験で、結合係数wが画像データになっているのは、そういう理屈)
この理論はDeepでも頻繁に出てくるので、わりと重要。
実装・R
2014/03/08 引数を修正2014/03/12 細かい修正
#使い方 if(FALSE){ library('bmp') data1 <- read.bmp('Downloads/mono/LENNA.bmp') data2 <- read.bmp('Downloads/mono/Cameraman.bmp') #実際には大きすぎてメモリが足りないので #dataの一部を小さく切り出してください data <- rbind(c(data1), c(data2)) tmp <- list(NULL) tmp$w <- NULL #学習 for(i in 1:10){ tmp <- rbm(train.mat=data,h.num=30,iter.num=10,w.mat=tmp$w,b.vec = tmp$b, c.vec = tmp$c) } #復元 huge <- list(NULL) for(i in 1:2){ huge[[i]] <- tmp$w %*% as.vector(data[i,] + rnorm(mean = 0, sd = 0.5, n = 111^2)) + tmp$c huge[[i]] <- 1 / ( 1 + exp( -huge[[i]] )) huge[[i]] <- t(tmp$w) %*% huge[[i]] + tmp$b huge[[i]] <- 1 / ( 1 + exp( -huge[[i]] )) image(matrix(huge[[i]], nrow=111)) } } #Restricted Boltzmann Machines rbm <- function(train.mat, h.num = 10, b.vec = NULL, c.vec = NULL, w.mat = NULL, iter.num = 2, learn.rate = 0.001){ #Sigmoid sigmoid <- function(x){ return( 1/(1+exp(-x)) ) } #Contrastive Divergence cd <- function(b.vec, h.vec, c.vec, w.mat, train.mat, iter.num = 2){ #勾配の初期化 dw.mat <- matrix(0, nrow = dim(w.mat)[1], ncol = dim(train.mat)[2]) dc.vec <- rep(0,dim(w.mat)[1]) db.vec <- rep(0,dim(train.mat)[2]) h.vec <- rep(0,dim(w.mat)[1]) dev.next() par(mar=c(0,0,0,0)) layout(matrix(1:(3*dim(w.mat)[1]*dim(train.mat)[1]),nrow = 3)) for(l in 1:dim(train.mat)[1]){ v.init.vec <- train.mat[l,] v.vec <- train.mat[l,] #step.vec <- rep(1,iter.num) step.vec <- seq(from=1000,to=1,length.out = iter.num+1) #初回のみhは0,1あとは確率値 #h.vec p1 <- (w.mat %*% v.vec + c.vec) #p1[-which.max(p1)] <- 0 #p1 <- (p1 - mean(p1))/sd(p1) p1 <- sigmoid( p1 ) h.vec <- rbinom(n=length(h.vec),size=1,prob=p1) #v.vec p1 <- ( t(w.mat) %*% h.vec + b.vec) #p1 <- (p1 - mean(p1))/sd(p1) p1 <- sigmoid( p1 ) v.vec <- p1 #calc grad pv0 <- sigmoid( ( w.mat %*% v.init.vec + c.vec) ) pvk <- sigmoid( ( w.mat %*% v.vec + c.vec) ) for(i in 1:length(pv0)){ image( matrix( (pv0 %*% c(v.init.vec))[i,], 28 ) ) image( matrix( w.mat[i,] , 28)) image( matrix( (pvk %*% c(v.vec))[i,], 28 ) ) } dw.mat <- dw.mat + pv0 %*% c(v.init.vec) - pvk %*% c(v.vec) dc.vec <- dc.vec + pv0 - pvk db.vec <- db.vec + v.init.vec - v.vec } ans <- list(dw.mat, db.vec, dc.vec) names(ans) <- c('dw','db','dc') return(ans) } dims.vec <- c(dim(train.mat)[2], h.num) if(is.null(w.mat)){ w.mat <- matrix(rnorm(mean=0,sd=0.001,n=prod(dims.vec)), nrow = dims.vec[2], ncol = dims.vec[1]) } p1 <- sigmoid( (w.mat%*% train.mat[1,] + 0) ) if(is.null(c.vec)){ c.vec <- log(abs((p1+0.01)/(1-p1))) # c.vec <- runif(min=-0.01,max=0.01,n=dims.vec[2]) } p1 <- sigmoid( (t(w.mat)%*%p1 ) ) if(is.null(b.vec)){ b.vec <- log(abs((p1+0.01)/(1-p1))) # b.vec <- rnorm(mean=0,sd=0.01,n=dims.vec[1]) } h.vec <- rep(0,dims.vec[2]) for(i in 1:dim(train.mat)[1]){ idx <- c(1:h.num) #idx <- sample(c(1:h.num),size=round(0.5 * h.num),replace=FALSE) hoge <- cd(b.vec,h.vec[idx],c.vec[idx],w.mat=w.mat[idx,],matrix(train.mat[i,],ncol=dim(train.mat)[2]),iter.num) w.mat[idx,] <- w.mat[idx,] + learn.rate * hoge$dw b.vec <- b.vec + learn.rate * hoge$db c.vec[idx] <- c.vec[idx] + learn.rate * hoge$dc } ans <- list(w.mat, b.vec, c.vec) names(ans) <- c('w','b','c') return(ans) } recover.rbm <- function(data.mat = NULL,para = NULL){ dev.next() par(mar=c(0,0,0,0)) layout(matrix(1:40,nrow = 4)) idx.vec <- list(sample(c(1:dim(data.mat)[1]),size=min(c(dim(data.mat)[1],10)),replace=FALSE), sample(c(1:dim(para$w)[1]),size=min(c(dim(para$w)[1],10)),replace=FALSE)) huge <- list(NULL) #for(i in 1:min(c(dim(data.mat)[1],10))){ for(i in 1:10){ image(matrix(data.mat[idx.vec[[1]][i],], nrow=sqrt(dim(data.mat)[2]))) image(matrix(para$w[idx.vec[[2]][i],], nrow=sqrt(dim(data.mat)[2]))) huge[[i]] <- para$w %*% data.mat[idx.vec[[1]][i],] + para$c huge[[i]] <- 1 / ( 1 + exp( -(huge[[i]]) )) huge[[i]] <- (t(para$w) %*% huge[[i]]) + para$b image(matrix(huge[[i]], nrow=sqrt(dim(data.mat)[2]))) huge[[i]] <- 1 / ( 1 + exp( -(huge[[i]]) )) image(matrix(huge[[i]], nrow=sqrt(dim(data.mat)[2]))) } }
ゼロから始めるDeepLearning_その3_ボルツマンマシンとは
はじめに
学部四年生向け。
ゼロから始めるDeepLearning_その1_ニューラルネットとは - 分からんこと多すぎ
→(Auto Encoder)
→(Denoising AutoEncoder)
→ゼロから始めるDeepLearning_その2_ホップフィールドネットワークとは
→ボルツマンマシン(この記事)
→Restricted ボルツマンマシン(後日)
→(Gaussian Binary - Restricted Boltzmann Machines)
→(Deep Belief Networks)
→(Deep Neural Networks)
→畳み込みニューラルネット(後日)
太線以外は読み飛ばしてOK
正直、RBMを使いたいだけなら、この記事は読まなくても問題ない。
ボルツマンマシン自体の資料が少なすぎて、この記事全体的に怪しい。
ボルツマンマシン
前回記事(ホップフィールドネットワーク)を読んでいることを全体とする。
ボルツマンマシンはホップフィールドネットワークのなら、みたいな部分を、
ボルツマン分布による確率的な処理に変えたものである。
(内部状態 y がそこそこだと50%の確率で出力xが1に変わり、
内部状態 y がすごく大きいと100%の確率で出力xが1に変わるイメージ)
ホップフィールドネットワークでは、初期値依存で記憶させた画像のうちのどれを思い出すのかが決まっていた。
ボルツマンマシンでは、確率的な処理により、初期値の依存性が減った。
(局所解に陥りにくくなった)
ちなみに、ボルツマン分布とは、ボルツマン分布 - Wikipedia曰く
"気体分子がとり得るエネルギー準位による分布の様子を表現した理論式"であり、こういう分布である。
(一応書いたけど見なくていい)
これをホップフィールドネットワークに取り込むと、以下のようになる。
0.初期の結合係数を相関行列などで決定し、
入力用の素子と出力用の素子を任意に選択する(以後固定)
(相関行列=データ行列とその転置の行列積を正規化したもの)
1.ランダムにノードiを選ぶ
2.出力xi=0の時のエネルギー準位をE0とする
出力xi=1の時のエネルギー準位をE1=E0-yiとする
3.ボルツマン分布より、p0=(xi=0となる確率)=
ボルツマン分布より、p1=(xi=1となる確率)=
4.確率にしたがって出力xiが変化する
(結合係数wを学習をする場合は、以下の5,6が加わる。
今回はこれに関して特に触れないが、学習と反学習と呼ばれる段階のこと)
5.ならば、
をわずかに増加させる。
6.入力素子に対するランダムな入力を行う。
この時、ならば、
をわずかに減少させる。
kTが大きい時はp0とp1は等しいので、状態は容易に変化する。


kTを徐々に小さくしていくと、p0とp1の差が大きくなり、定常状態に至る。
(確率分布なので、ある1つの状態に落ち着くわけではない。
各状態の出現頻度がある1つの確率分布に従うようになる)


なお、このように、あるノードの状態がまわりのノードからの影響のみによって、
確率的に変化するという性質を「場のマルコフ性」という。
このような性質を持つ無向グラフを、マルコフ確率場Markov random fieldと呼ぶ。
マルコフ確率場の考えは、画像の分野では頻繁に登場し、画像修復や領域分割に用いられる
ホップフィールドネットワークの時の結合係数wは、ユーザが設定し、以後変更しないものだった。
このような場合、記憶させるイメージの数が増えてくると、
局所解に陥り記憶させたネットワークの状態に至れないことがある。
(偽記憶と呼ばれる平衡状態に陥る)
それに対してボルツマンマシンは温度変化による状態遷移(焼きなまし法)であり、
局所解からの脱出が可能になったところが、ホップフィールドネットワークより優位である。
また、手動での設計が困難な、より良い結合係数wを探索するアルゴリズムでもある。
何より理論解析が色々できるようになったことが楽しい。
ボルツマンマシンとギブスサンプラー
ボルツマンマシンの状態変化は、ギブスサンプラー(Markov Chain Monte Carlo algorithm)であると言うこともできる。
要するに、ある更新前の出力を、ある確率分布Pに入れると、
更新後の出力のi番目の要素の出力が出てくる確率を教えてくれる分布Qを作れるということ。
これはアルゴリズムの更新に用いている分布と一致する。
つまり、上で紹介したアルゴリズムは、中でギブスサンプラーを回していることになる。
ボルツマンマシンの更新は、一時刻前のネットワークの状態によってのみ定まるので、
一次のマルコフ連鎖とも言える。
そのため、ボルツマンマシンを長時間動作させたあとの状態は、
ネットワークの初期値(最初に見せるイメージ)によらない。
(変化規則の元になった分布関数に近づくという定理があるらしいです)
次回でようやくRestrictedボルツマンマシンの話。